Information and physics: what's the status of the quantum computer?
IN "CLASSICAL" PHYSICS, INFORMATION IS ABSENT FROM THE BASIC CONCEPTS
Some sociologists like to say that we have moved towards an information society. In France, we speak of a "digital society". But what exactly is information? It is often defined as a sequence of symbols 0 and 1, and characterizes the choice available to the sender of the message who sends this sequence. The notion of information has as its counterpart Shannon's notion of entropy, which takes the point of view of the messenger of the sequence, who would not know the message's code. But these abstract considerations only provide a mathematical definition of information. What do these symbols 0 and 1 correspond to in practical terms, at the level of a physical device? Classical physics, such as Newton's Law, applies to continuous variables such as position, velocity, force and momentum. Representing a bit, an intrinsically discrete entity, by a physical state in the context of continuity, is not self-evident. The pioneer of statistical mechanics, Ludwig Boltzmann, came up against this problem when he foresaw the link between thermodynamic entropy and information. The problem was eloquently transformed into a paradox by 19th-century physics genius James Clerk Maxwell, who told the story of the miraculous feats of an imaginary demon capable of seeing molecules and exploiting their disordered motion. But let's return to the practical problem of the concrete implementation of the symbols 0 and 1. In the central processing unit of one of our desktop computers, the working memory encodes the symbols 0 and 1 by the two states of a bistable electrical circuit comprising at least four interconnected transistors. Seen from one of these transistors, the two states correspond to the circulation or non-circulation of electric current. This circuit is the electrical equivalent of a flip-flop (see illustration below) .
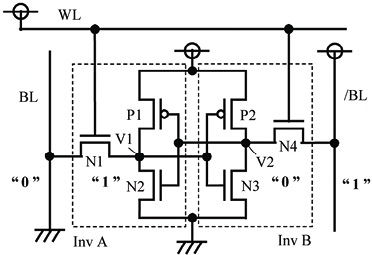
Top: flip-flop circuit with six CMOS transistors, capable of encoding 1 bit. Bottom: bistable mechanical equivalent encoding one binary digit.
The dissipative nature of the circuit is crucial to ensuring information stability and rapid access. The counterpart of these properties is their energy consumption: on the order of 10% of the energy of the economies of the so-called "developed" countries is today devoted to communication and information processing. Classical mechanics cannot fully analyze the theoretical limit of energy consumption for the operations involved in storing, propagating and transforming information. But classical physics has been supplanted by so-called "quantum physics", which itself has a close and natural relationship with information theory. The need to change the fundamentals of physics arose at the end of the 19th century with the so-called "blackbody radiation" problem, which for the first time in several centuries strongly challenged the then triumphant classical physics. Classical physics predicted that the inside of an oven, heated red-hot by an internal electrical resistor and communicating with the outside through a small transparent window, would have to emit an infinite amount of luminous radiation through the window, in flagrant contradiction to experience and, of course, common sense. To resolve this contradiction, the German theoretical physicist Max Planck introduced a new constant of nature, the quantum of action, which now bears his name. The young Albert Einstein intuitively understood that Planck's constant limited the maximum amount of information that could be stored in a physical system. The construction of quantum physics, and its links with information theory, had begun.
HOW QUANTUM MECHANICS PUTS INFORMATION ON THE TABLE OF FUNDAMENTAL PHYSICAL QUANTITIES
Let's take an oscillator, for example a rigid pendulum, like the pendulum of a Comtoise clock. This is the simplest physical system, and allows us to discuss the difference between classical and quantum physics without too many mathematical complications. It has a single degree of freedom: the angle between the pendulum axis and the vertical. Classically, all the dynamic variables of the pendulum are continuous: angle, energy, angular momentum, etc. In quantum mechanics, this system acquires a single degree of freedom. In quantum mechanics, this system acquires a discrete character. You might object that a pendulum is a macroscopic object far removed in size from atoms and molecules. But quantum mechanics is a universal theory that applies to all systems, regardless of their size. Moreover, there are electrical systems whose equations of motion are exactly the same as those of the pendulum. It is therefore entirely legitimate to take an interest in the so-called stationary states of a quantum pendulum. This is achieved by compensating the residual friction of the pendulum with an external input of energy, as achieved by the clock's escapement mechanism, itself powered by the falling weights being wound. Unlike the stationary states of a classical oscillator, where the energy can take on any positive value, the energy of a quantum oscillator adopts discrete values given by the ratio between Planck's constant and the oscillator's period. In practice, for the Comtoise clock, the oscillation period is so large (1 second) and Planck's constant so small (of the order of 10-34 Joule.second) that the discretization effect is entirely unobservable. On the other hand, the oscillation corresponding to the movement of electrons in an atom is much faster, and the discretization of motion that can then be observed is the basis of our atomic clocks. Thus, in quantum mechanics, a finite volume of matter and fields, whose total energy is bounded, can only contain a finite amount of information. The same situation, in classical mechanics, will either yield an infinite quantity of information, or a quantity of information fixed by circumstantial technical details devoid of fundamental meaning.
Quantum theory predicts other profound properties linking physics and information. A basic law of quantum physics states that the information imparted to a system is conserved in all basic microscopic processes, and this law seems to transcend all others. Physicists such as John Archibald Wheeler have even put forward the idea that information is the basic quantity of physics, and that it would be possible to base all others on it. This research program even spawned a slogan: from bit to it. From this law of conservation, we can derive the notion of information flow, and its limit. For a given available transmission power, we can't exceed a maximum number of bits per second set by Planck's constant, currently seen as the second fundamental constant of physics after the speed of light. In a publication aimed at telecom engineers, I can't resist writing this formula:
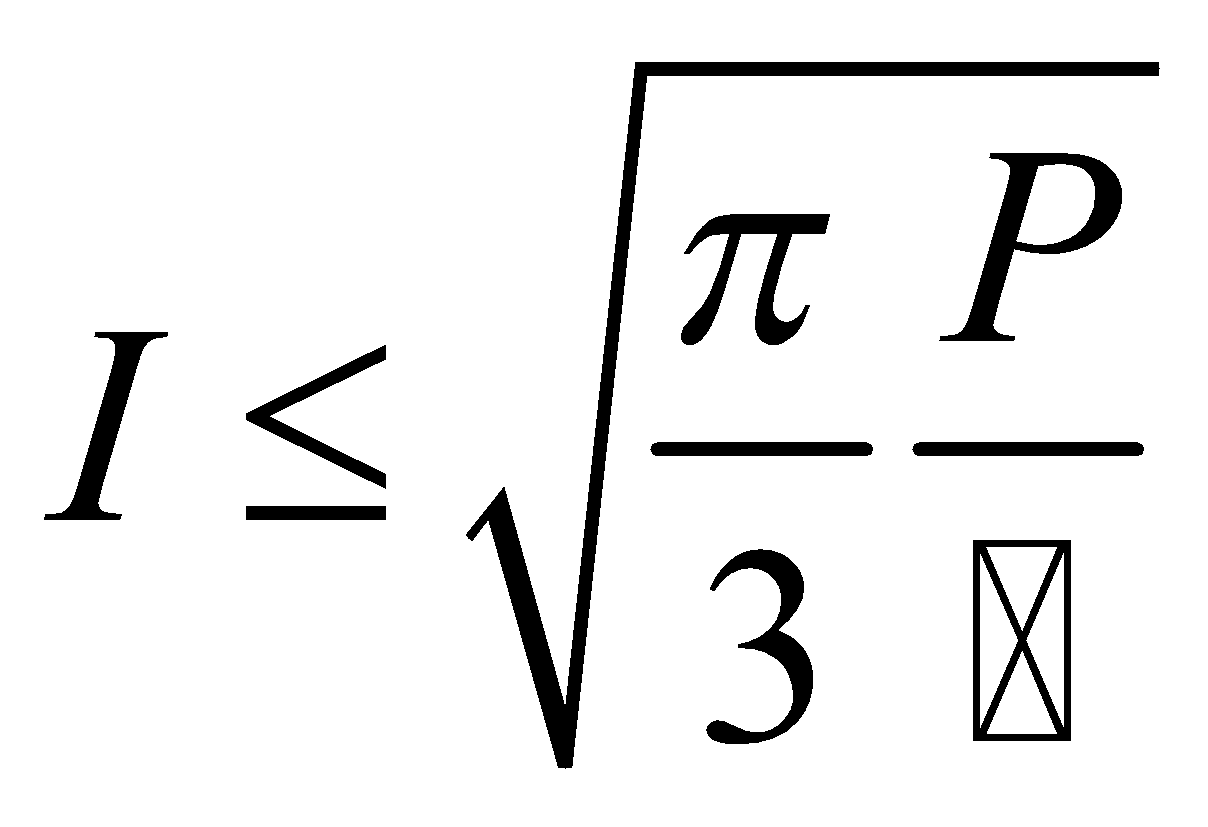
where I is the information flow in bits per second, P is the available transmission power in watts, and ћ is Planck's reduced constant. Applying this formula to today's digital communication systems, we can see just how much energy our information processing wastes, compared with the theoretical optimum. By comparison, the steam locomotive, the subject of Sadi Carnot's preoccupation with the thermodynamic efficiency of heat-to-work conversion, is a marvel of economy!
THE CONCEPT OF THE QUANTUM COMPUTER BEFORE THE TURNING POINT IN 1994
In the second half of the twentieth century, as miniaturization progressed, physicists gradually realized that the electronic workings of a computer could be reduced to single atoms, or perhaps even elementary particles. But, at this point in history, the ambition of physicists was limited to the theoretical demonstration that such an extremely miniaturized computer could, on paper, continue to function as well as a conventional computer. Indeed, the physicists who wanted to apply the concepts of quantum physics to the nascent science of computing were hampered by a basic principle of quantum theory that seemed to them a serious obstacle to the ultimate miniaturization of information processing systems: Heisenberg's uncertainty principle. While the discretization of an oscillator's energy levels seems to be more in line with the assumptions of computer science, the uncertainty principle seems to depart radically from them, as it seems to stipulate that there is a fundamental noise in nature that we can't get rid of. What exactly is this uncertainty principle formulated by Werner Heisenberg? The simplest statement involves a free particle in uniform rectilinear motion, with only the axis of its trajectory known. At any given moment, neither the position nor the velocity of the particle on this axis is known exactly. The uncertainty principle stipulates that if we measure the particle's velocity, for example using the Doppler effect, the position of the particle will be subject to feedback noise from the measuring instrument, the greater the velocity resolution. Conversely, if we measure the particle's position, for example by observing its passage through a light beam perpendicular to its trajectory, its velocity will fluctuate the more the position resolution is small. The product of errors in position and velocity will always be greater than a factor given by Planck's constant, divided by the particle's mass. It's the enormous mass of the objects around us, expressed in quantum units, that prevents us from perceiving this blur imposed by the uncertainty principle. The fluctuations resulting from measurement, which blur position and velocity, correspond to uncontrollable parasitic forces of a fundamental nature. They will remain present even if the measuring device is perfect. Fortunately, what physicists realized in the 1980s was that computer logic gates, reduced to elementary particles, can in principle function perfectly, since it is possible to bypass the constraints imposed by the uncertainty principle, since calculation obeys different rules from measurement. In the final analysis, the uncertainty principle in no way limits the precision of calculations, even if Planck's constant places limits on the speed of information processing, for the energy involved. At the same time, these discoveries completed Boltzmann's work and established that "heat = energy + lack of information", thus resolving Maxwell's demon paradox. So, in the 1980s, useful quantum calculations with quantum bits (qubits, see illustration below) and quantum logic gates were still out of the question. Only Richard Feynman foresaw the possibility that a machine using quantum mechanics could be useful as a simulator of the behavior of matter at the microscopic level.
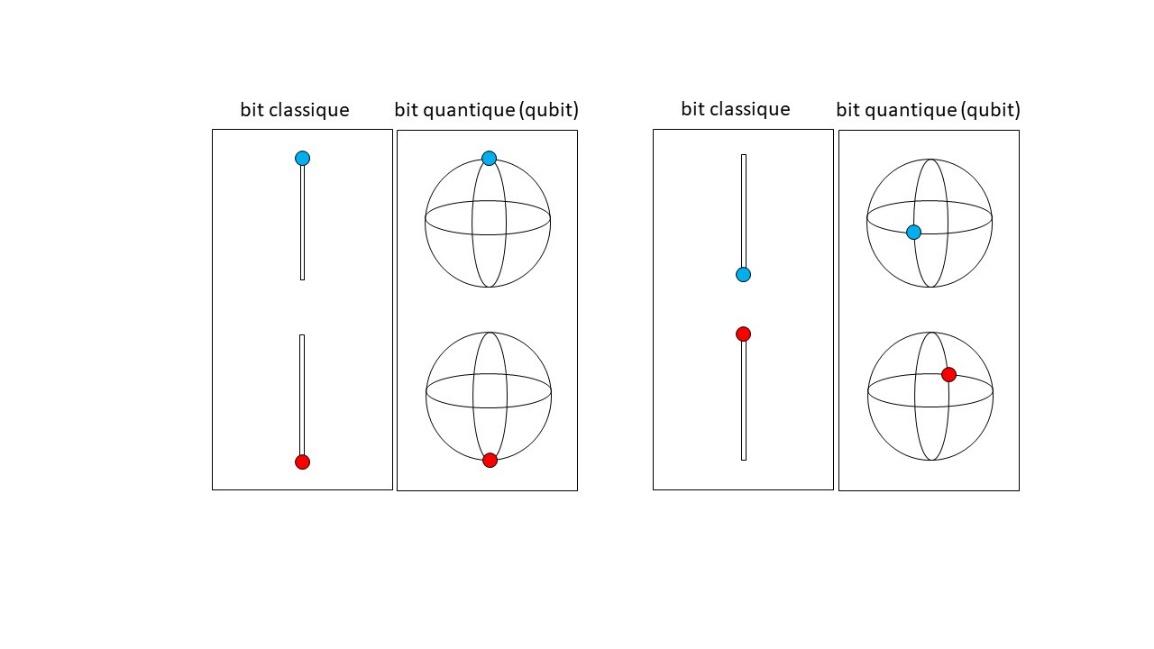
Left panels: a classic bit can be found in two configurations, represented by a point forced to lie at the ends of a segment. The point is colored blue if its configuration represents 0, and red if its configuration represents 1. Qubit configurations, on the other hand, are represented by two antipodal points on a sphere.
Right panels: when changing the encoding of the classical bit, the only possibility is to exchange the roles of 0 and 1. For the qubit, a continuous variety of antipodal point pairs can be chosen on the sphere. Here, a pair of points placed on the equator has been represented, but a different latitude and longitude could just as easily have been chosen. This continuous freedom of qubits, which increases exponentially with the number of qubits in a register, is known as the "superposition principle". It makes qubits more powerful than conventional bits.
THE TWO DISCOVERIES OF PETER SHOR, FOUNDING FATHER OF MODERN QUANTUM INFORMATION
A few years later, in 1994, Peter Shor, a mathematician at MIT in Boston, proposed a new algorithm for factoring a number into its prime factors. This factorization is very important, both conceptually and practically. It's the simplest example of an asymmetric function. It's very quick to multiply two prime numbers. On the other hand, it's very difficult, knowing only their product, to go back to the two starting numbers. This asymmetry is the basis for encoding sensitive information on the Internet, such as credit card codes or medical information. Peter Shor mathematically demonstrates that his new algorithm, which can only be executed by a hypothetical quantum computer, would exponentially beat the best classical algorithm. To the astonishment of computer scientists, this new algorithm classified factoring as a so-called easy problem, i.e. one whose execution time increases polynomially with the number N of digits in the problem statement. Difficult problems are those where the execution time grows as an exponential function of N, which seems to be the case for factoring. The reason for this astonishment is that it was previously believed that an algorithm had an intrinsic complexity, a complexity measured by a power of N that was independent of the machine on which the algorithm was run, even if different technologies could change a numerical pre-factor in the expression of the execution time.
But the enthusiasm of computer scientists was short-lived, as it seemed that Peter Shor's demonstration of the N3 quantum complexity of his quantum algorithm implied that, for the algorithm to work, the machine had to be perfect. It was to address this point that Peter Shor conceived a second invention, which would really launch the subject of quantum information: like classical computers, quantum computers can very well be built with imperfect parts, which are therefore prone to error. This second discovery is even more extraordinary than the first. It is now considered by some to be the great quantum discovery of the late 20th century. It demonstrates that it is theoretically possible to design a process - known as quantum error correction - that can repair the influence of noise and hardware imperfections, something that many physicists believed was forbidden by the laws of physics. These physicists based their argument on Heisenberg's famous uncertainty principle (again, but in a slightly different role), which seems to give measurement a necessarily intrusive and random character. They objected that to correct was to take cognizance of the errors, i.e. to carry out a measurement, which would necessarily lead to a disturbance, which would lead to new errors, so that the correction process could not converge.
Peter Shor's diabolical trick is also based on circumventing the uncertainty principle. He understands that, in quantum physics, it is entirely possible to detect that an error has occurred in the system and to know where, without needing to take direct cognizance of the information that is encoded, which classical reasoning believes to be necessary (see box on the principle of quantum correction).
THE ADVENTURE OF IMPLEMENTING QUANTUM MACHINES
Since then, various teams of physicists around the world (USA, Canada, Europe, China, India, Australia) have succeeded not only in realizing qubits, but also in making them interact to perform logic gates. Recently, the team at my laboratory at Yale succeeded in demonstrating that error correction could work in practice, which is an essential step. The best-performing systems at present are those based on superconducting circuit chips with Josephson junctions, and those based on arrays of atoms levitated in vacuum. In the latter approach, the atoms are individually controlled by laser beams. Other possible technologies include integrated fiber optic chips and isolated spin qubits in semiconductors. No one has yet succeeded in building machines that exceed the order of magnitude of a thousand qubits interconnected by quantum gates. This is to be compared with the tens of billions of transistors on a laptop chip... Yet progress is constant, year after year, if we include all international research, financed to the tune of a few billion dollars a year for a country like the USA (compared with the tens of billions a year invested in semiconductor chips). Even if progress is slower than investors would like, there has not yet been a quantum "winter", as has been the case with artificial intelligence, which has progressed in stages since the 1960s. To date, no principle of physics has been discovered that prohibits the realization of a quantum computer of arbitrary size. Before discussing the possible applications of quantum machines, let's take a closer look at their basic principles and try to understand the advantage they can offer in information processing.
HOW DO QUBITS WORK, AND HOW DO THEY DIFFER FROM CONVENTIONAL BITS?
Journalists usually answer these questions by first invoking the principle of superposition. According to the current expression in the media, qubits could be in both 0 and 1 states. This last phrase is a gross simplification, because reading a qubit always gives a result that can only be 0 or 1, just like reading a conventional bit.
The correct explanation of the differences between classical and quantum bits involves the notion of coding, which is discrete in the classical case, and continuous in the quantum case, allowing the observation of interference, as we can take the different paths that exist from one point of a sphere to another (see illustration on page 15).
More generally, there are several fundamental differences between a machine processing classical information and one processing quantum information:
- If the same algorithm - in the sense of a sequence of logic gates - is repeated on a classical machine with the same starting data, the end result is always the same. But if the same program is repeated on a quantum machine, the measurement of the final result does not always give the same values and presents a statistical distribution with correlations of a type unattainable by a classical machine.
- The relationship between initial data and final data obeys a new logic, quantum logic, which happens to be that of nature, and not the one formulated by ancient Greek mathematicians. The classical logic of the Greeks is "degenerate" compared to quantum logic, which, for example, does not forbid the friends of our friends to be our enemies. Indeed, quantum correlations do not obey the same transitivity theorems as classical correlations.
- The quantum computer seems to derive its power from exploiting the phenomenon of entanglement, which enables information to be encoded in a non-local manner. One bit of quantum information can, in principle, be relocated to several machines at once, without being copied in the slightest, and could even be simultaneously stored at two points on Earth several thousand kilometers apart (current record = several tens of kilometers).
The special properties of quantum information give quantum computers the ability to solve certain problems unsolvable by conventional computers, or to build communications networks whose security is guaranteed by the laws of physics. But the most convincing applications of quantum information are those that apply to the quantum world itself. Feynman's proposal has now been confirmed: the quantum computer could perform calculations for the design of new molecules in chemistry and pharmacology, and in the creation of new materials. Quantum information-processing machines could also prove very useful for high-precision measurements, such as the detection of gravitational waves, or highly sensitive measurements of very small quantities of matter, such as the imaging of individual molecules. There is now little doubt that quantum information will provide powerful tools for fundamental research in the future.
INDUSTRIAL APPLICATIONS OF QUANTUM INFORMATION
The successes achieved in the academic world in experimentally verifying the basic concepts of quantum information have aroused the interest of major companies in the digital economy (Google, IBM, Intel, Microsoft, Amazon, etc.) and led to the creation of dozens of start-ups. Will the adage "If it is beautiful, it is useful" hold true for society as a whole? While a quantum industry is already taking shape, hopes of large-scale commercial applications remain hypothetical for the time being. But the public has already noticed that the big Internet companies are themselves building the social environment that makes them indispensable. Will they be able to ensure, for example, that one day we won't be able to do without quantum games and entertainment? And let's not forget that the first practical application of the principles of quantum physics was a proposal for quantum money based on the property of quantum information that it cannot be copied - in other words, it cannot be completely dematerialized, even if it can be teleported over great distances using entanglement. Perhaps the real large-scale application of quantum computers is the advanced security of our personal data?
Quantum error correction
First, let's take the example of a classical bit that can randomly flip over from time to time, creating an error, called a bit-flip (we're assuming here that this is the only possible error). We can protect the information as follows. Let's use three physical bits to encode one logical bit. The logical 0 will be encoded by the physical triplet 000, and the logical 1 will be encoded by the physical triplet 111. We can see that, even if an error occurs on one of the physical bits, we'll still be able to recover the initial information. In fact, if we can be sure that only one bit error has occurred, we only need to count the number of 0's and 1's in the triplet to reconstitute the original configuration. The following table summarizes the error correction process. The left-hand column shows what was read from the register, and the right-hand column the value after correction.
|
000 |
→ |
000 |
|
001 |
→ |
000 |
|
010 |
→ |
000 |
|
100 |
→ |
000 |
|
110 |
→ |
111 |
|
011 |
→ |
111 |
|
101 |
→ |
111 |
|
111 |
→ |
111 |
But in quantum mechanics, this strategy cannot be used. Even if going from 1 to 3 qubits is beneficial (redundancy), reading the qubit's information content directly destroys the quantum information, according to the uncertainty principle. A trick is needed. The solution is to measure the sum modulo 2 (here called S12) of the first two qubits, then the sum modulo 2 (here called S23) of the last two qubits. This provides the information needed to correct the qubit at fault, without having to read the information directly. The table below shows the four possible outcomes of the measurement of the two modulo 2 sums, without disturbing the qubits.
|
S12 = 0,S23 = 0 |
→ |
do nothing |
|
S12 = 0,S23 = 1 |
→ |
pinball qubit 3 |
|
S12 = 1,S23 = 0 |
→ |
pinball qubit 1 |
|
S12 = 1,S23 = 1 |
→ |
pinball qubit 2 |
It has been assumed here that only one quantum flip occurs in the triplet. Here, the qubit flip corresponds to a rotation of the sphere of the figure above around an axis passing through the equator. But we can also have a phase-flip error, corresponding to a rotation around an axis passing through the pole. If we want to correct both bit-flips and phase-flips, we need even more redundancy. The historical code invented by Peter Shor comprised nine qubits. More recent research has shown that the theoretical minimum is five physical qubits for one logical qubit. More sophisticated error-correcting codes have also been theoretically invented, such as the so-called "surface code" comprising hundreds of qubits per logic qubit. In these latter codes, not only memory but also logic operations are protected from errors. At the time of writing, the protection of logical operations - the keystone of quantum computer applications - has yet to be put into practice.
Read more
Julien Bobroff, "La nouvelle révolution quantique", Flammarion, 2022
Carlo Rovelli, "Helgoland", Champs, 2023
Scott Aaronson, "Quantum computing since Democritus", Cambridge University Press, 2013
Assa Auerbach, "Max the demon", Amazon, 2017

Michel DEVORET (1975)
After completing the DEA in Quantum Optics, Atomic and Molecular Physics at Université Paris XIII Orsay in his final year at Télécom, Michel Devoret defended his post-graduate thesis in this field, then branched out into solid state physics for his PhD thesis at the same university. After a post-doctoral stay at the University of California at Berkeley, he founded his own research group on superconducting quantum circuits at CEA-Saclay, with Daniel Esteve and Cristian Urbina. In 2002, he became a professor at Yale University. He also taught at the Collège de France from 2007 to 2012. Michel Devoret is a member of the Académie des Sciences (France) and the National Academy of Sciences (USA).
Author