Information et physique : où en est l’ordinateur quantique ?
EN PHYSIQUE DITE « CLASSIQUE », L’INFORMATION EST ABSENTE DES CONCEPTS DE BASE
Certains sociologues aiment dire que nous avons transité vers une société de l’information. En France, on parle de « société numérique ». Mais qu’est-ce au juste que l’information ? On la définit souvent à partir d’une suite de symboles 0 et 1, et elle caractérise le choix dont dispose l’expéditeur du message qui envoie cette suite. La notion d’information a pour contrepartie la notion d’entropie de Shannon, qui elle, prend le point de vue du messager de la suite, qui ne connaîtrait pas le code du message. Mais ces considérations abstraites ne donnent qu’une définition mathématique de l’information. À quoi correspondent ces symboles 0 et 1 sur le plan pratique, au niveau d’un dispositif physique ? La physique « classique », comme celle de la loi de Newton par exemple, s’applique à des variables continues, comme la position, la vitesse, la force et la quantité de mouvement. Représenter un bit, entité intrinsèquement discrète, par un état physique dans le contexte du continu, ne va pas de soi. Le pionnier de la mécanique statistique, Ludwig Boltzmann, se heurta à ce problème quand il pressentit le lien entre entropie thermodynamique et information. Le problème fut éloquemment transformé en paradoxe par le génie de la physique du 19ème siècle, James Clerk Maxwell, qui raconta l’histoire des prouesses miraculeuses d’un démon imaginaire capable de voir les molécules et d’exploiter leur mouvement désordonné. Mais revenons au problème pratique de l’implémentation concrète des symboles 0 et 1. Dans l’unité centrale d’un de nos ordinateurs de bureau, la mémoire de travail encode les symboles 0 et 1 par les deux états d’un circuit électrique bistable comportant au moins quatre transistors interconnectés. Vu de l’un de ces transistors, les deux états correspondent à la circulation ou la non-circulation de courant électrique. Ce circuit est l’équivalent électrique d’une bascule (voir illustration ci-dessous).
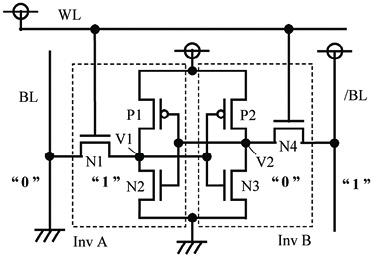
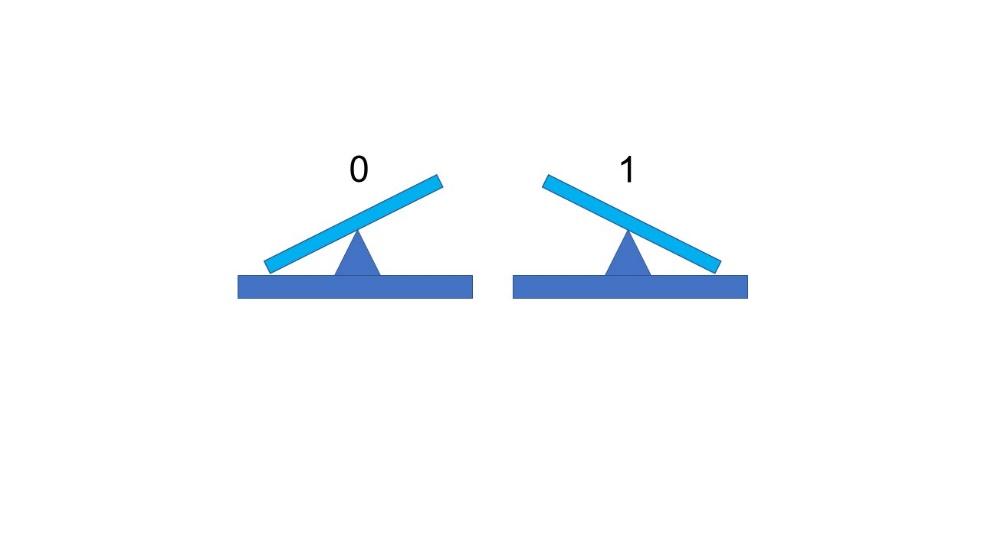
En haut : circuit bascule comportant six transistors CMOS et pouvant encoder 1 bit. En bas : équivalent mécanique bistable encodant un chiffre binaire.
Le caractère dissipatif du circuit est crucial pour assurer la stabilité de l’information, ainsi que son accès rapide. La contrepartie de ces propriétés est leur consommation d’énergie : de l’ordre de 10 % de l’énergie des économies des pays dits « développés » est aujourd’hui consacrée à la communication et au traitement de l’information. La mécanique classique ne peut pas analyser complètement la limite théorique de consommation d’énergie pour les opérations impliquées dans le stockage, la propagation et la transformation de l’information. Mais la physique classique a été supplantée par la physique dite « quantique », qui, elle, entretient un rapport étroit et naturel avec la théorie de l’information. Le besoin de changer les bases de la physique est apparu à la fin du XIXe siècle avec le problème dit du « rayonnement du corps noir », qui, pour la première fois depuis plusieurs siècles, remettait fortement en question la physique classique, alors triomphante. La physique classique prédisait que l’intérieur d’un four, chauffé au rouge par une résistance électrique interne et communiquant avec l’extérieur par une petite fenêtre transparente, devrait émettre par la fenêtre une quantité infinie de rayonnement lumineux, en contradiction flagrante avec l’expérience, et, bien entendu, avec le bon sens. Pour résoudre cette contradiction, le physicien théoricien allemand Max Planck introduisit une nouvelle constante de la nature, dite du quantum d’action, qui porte maintenant son nom. Le jeune Albert Einstein comprit alors intuitivement que la constante de Planck limitait la quantité d’information maximale qui pouvait être stockée dans un système physique. La construction de la physique quantique, et ses liens avec la théorie de l’information, commençaient.
COMMENT LA MÉCANIQUE QUANTIQUE FAIT ASSEOIR L’INFORMATION À LA TABLE DES QUANTITÉS FONDAMENTALES DE LA PHYSIQUE
Prenons un oscillateur, par exemple un pendule rigide, comme le balancier d’une horloge comtoise. C’est le système physique le plus simple, et il permet de discuter la différence entre physique classique et quantique sans trop de complications mathématiques. Il possède un seul degré de liberté : l’angle que fait l’axe du pendule avec la verticale. Classiquement, toutes les variables dynamiques du pendule sont continues : angle, énergie, moment angulaire, etc. En mécanique quantique, ce système acquiert un caractère discret. Vous pourriez objecter qu’un pendule est un objet macroscopique fort éloigné en taille des atomes et des molécules. Mais la mécanique quantique est une théorie universelle qui s’applique à tous les systèmes, indépendamment de leur taille. Du reste, il existe des systèmes électriques dont les équations du mouvement sont exactement les mêmes que celles du pendule. Il est donc tout à fait légitime de nous intéresser aux états dits stationnaires d’un pendule quantique. Ils sont associés à une oscillation se répétant à l’identique périodiquement, obtenue en compensant la friction résiduelle du pendule par un apport externe d’énergie, ce que réalise le mécanisme d’échappement de l’horloge, lui-même alimenté par la chute des poids que l’on remonte. Contrairement aux états stationnaires d’un oscillateur classique où l’énergie peut prendre n’importe quelle valeur positive, l’énergie de l’oscillateur quantique adopte, elle, des valeurs discrètes données par le rapport entre la constante de Planck et la période de l’oscillateur. En pratique, pour l’horloge comtoise, la période d’oscillation est si grande (1 seconde) et la constante de Planck si petite (de l’ordre de 10-34 Joule.seconde) que l’effet de discrétisation est entièrement inobservable. En revanche, l’oscillation correspondant au mouvement des électrons dans un atome est beaucoup plus rapide, et la discrétisation du mouvement que l’on peut alors observer est à la base de nos horloges atomiques. Ainsi, en mécanique quantique, un volume fini de matière et de champs, dont l’énergie totale est bornée, ne pourra contenir qu’une quantité d’information finie. La même situation, en mécanique classique, donnera ou bien une quantité d’information infinie, ou bien une quantité d’information fixée par des détails techniques circonstanciels et dénués de signification fondamentale.
La théorie quantique prédit d’autres profondes propriétés reliant physique et information. Une loi de base de la physique quantique stipule que l’information impartie à un système est conservée dans tous les processus microscopiques de base, et cette loi semble d’ailleurs transcender toutes les autres. Des physiciens comme John Archibald Wheeler ont même émis l’idée que l’information est la quantité de base de la physique, et qu’il serait possible d’asseoir toutes les autres sur elle. Ce programme de recherche a même engendré un slogan : from bit to it. De cette loi de conservation, on peut dériver la notion de flux d’information, ainsi que sa limite. Pour une puissance d’émission disponible donnée, on ne peut pas dépasser un nombre maximal de bits par seconde fixé par la constante de Planck, actuellement vue comme la deuxième constante fondamentale de la physique après celle de la vitesse de la lumière. Je ne peux pas, dans une publication destinée aux ingénieurs Télécom, résister à l’écriture de cette formule :
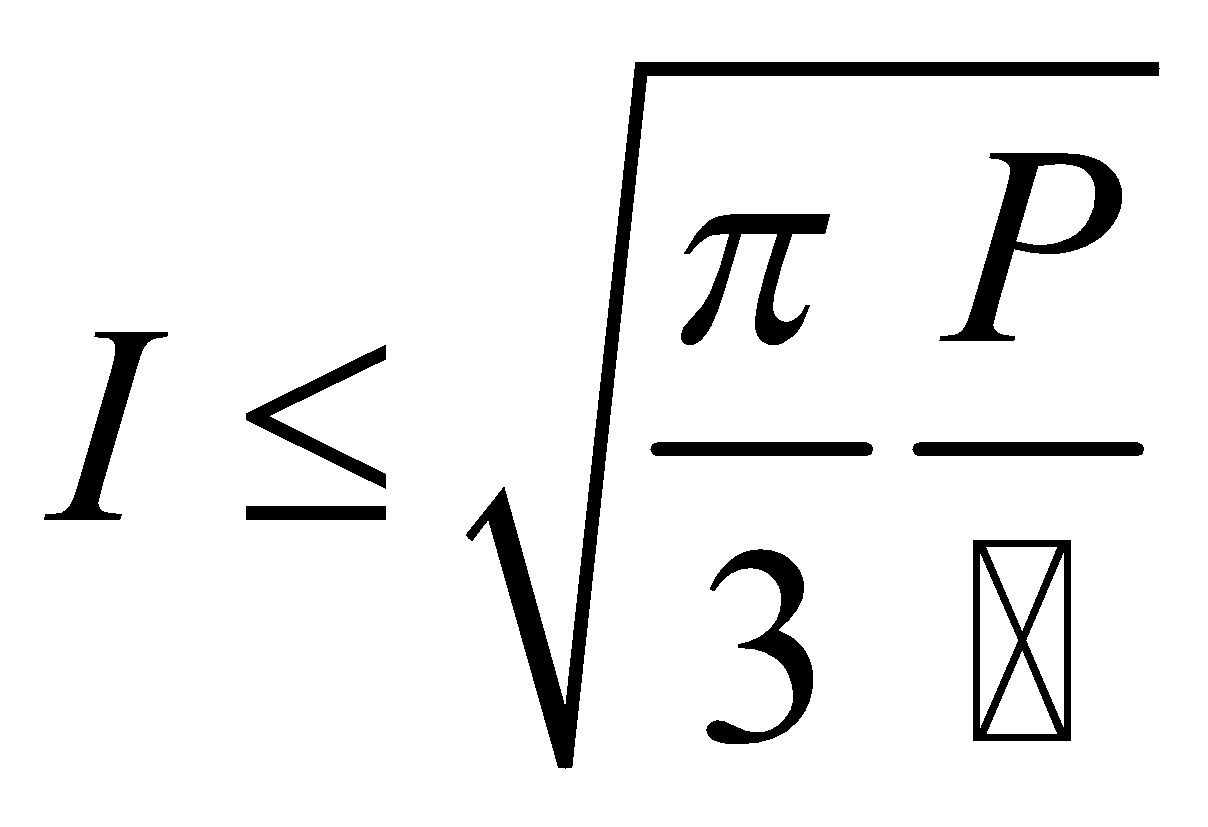
dans laquelle I est le flux d’information en bits par seconde, P est la puissance en watt de transmission dont on dispose, et ћ la constante de Planck réduite. L’application de cette formule aux systèmes de communication numérique en place aujourd’hui permet de comprendre à quel point notre traitement de l’information gaspille l’énergie, par rapport à l’optimum théorique. Par comparaison, la locomotive à vapeur, sujet de la préoccupation de Sadi Carnot sur le rendement thermodynamique de conversion de chaleur en travail, est une merveille d’économie !
LE CONCEPT D’ORDINATEUR QUANTIQUE AVANT LE TOURNANT DE 1994
Dans la seconde moitié du XXe siècle, avec les progrès de la miniaturisation, les physiciens ont, petit à petit, pris conscience que les rouages électroniques d’un ordinateur pourraient être réduits à des atomes uniques ou peut-être même à des particules élémentaires. Mais, à ce moment de l’histoire, l’ambition des physiciens se limita à la démonstration théorique qu’un tel ordinateur miniaturisé à l’extrême pourrait, sur le papier, continuer à fonctionner aussi bien qu’un ordinateur conventionnel. En effet, les physiciens qui voulaient appliquer les concepts de la physique quantique à la science naissante de l’informatique, étaient gênés par un principe de base de la théorie quantique qui leur paraissait un sérieux obstacle à la miniaturisation ultime des systèmes de traitement de l’information : le principe d’incertitude d’Heisenberg. Si la discrétisation des niveaux d’énergie d’un oscillateur paraît plutôt s’aligner avec les hypothèses de l’informatique, le principe d’incertitude semble s’en éloigner radicalement, car il a l’air de stipuler qu’il existe dans la nature un bruit fondamental dont on ne peut se débarrasser. Quel est au juste ce principe d’incertitude formulé par Werner Heisenberg ? Son énoncé le plus simple fait intervenir une particule libre en mouvement rectiligne uniforme, dont on ne connaît que l’axe de la trajectoire. À un instant donné, on ne connaît exactement ni la position, ni la vitesse de la particule sur cet axe. Le principe d’incertitude stipule que si l’on mesure la vitesse de la particule, par exemple en utilisant l’effet Doppler, la position de la particule va subir de la part de l’instrument de mesure un bruit en retour sur la position d’autant plus grand que la résolution sur la vitesse est petite. Réciproquement, si on mesure la position de la particule, par exemple en observant sa traversée d’un rayon lumineux perpendiculaire à sa trajectoire, sa vitesse va subir en retour une fluctuation d’autant plus grande que la résolution en position est petite. Le produit des erreurs en position et en vitesse va toujours être supérieur à un facteur donné par la constante de Planck, divisée par la masse de la particule. C’est la masse énorme des objets qui nous entourent, exprimée en unités quantiques, qui nous empêche de percevoir ce flou imposé par le principe d’incertitude. Les fluctuations résultant de la mesure, qui floutent position et vitesse, correspondent à des forces parasites incontrôlables de nature fondamentale. Elles resteront présentes même si l’appareil de mesure est parfait. Heureusement, ce que réalisent les physiciens des années 1980, c’est que les portes logiques de l’ordinateur, réduites à des particules élémentaires, peuvent en principe fonctionner parfaitement, car il est possible de contourner les contraintes imposées par le principe d’incertitude, le calcul obéissant à des règles différentes de celle de la mesure. En fin de compte, le principe d’incertitude ne limite en rien la précision des calculs, même si la constante de Planck met des bornes à la vitesse de traitement de l’information, pour une énergie mise en jeu. En parallèle, ces découvertes achèvent l’œuvre de Boltzmann et établissent que « chaleur = énergie + manque d’information », résolvant ainsi le paradoxe du démon de Maxwell. Ainsi, dans les années 80, il n’est pas encore question de faire des calculs quantiques utiles avec des bits quantiques (qubits, voir illustration ci-dessous) et des portes logiques quantiques. Seul Richard Feynman entrevoit la possibilité qu’une machine utilisant la mécanique quantique pourrait être utile en tant que simulateur du comportement de la matière au niveau microscopique.
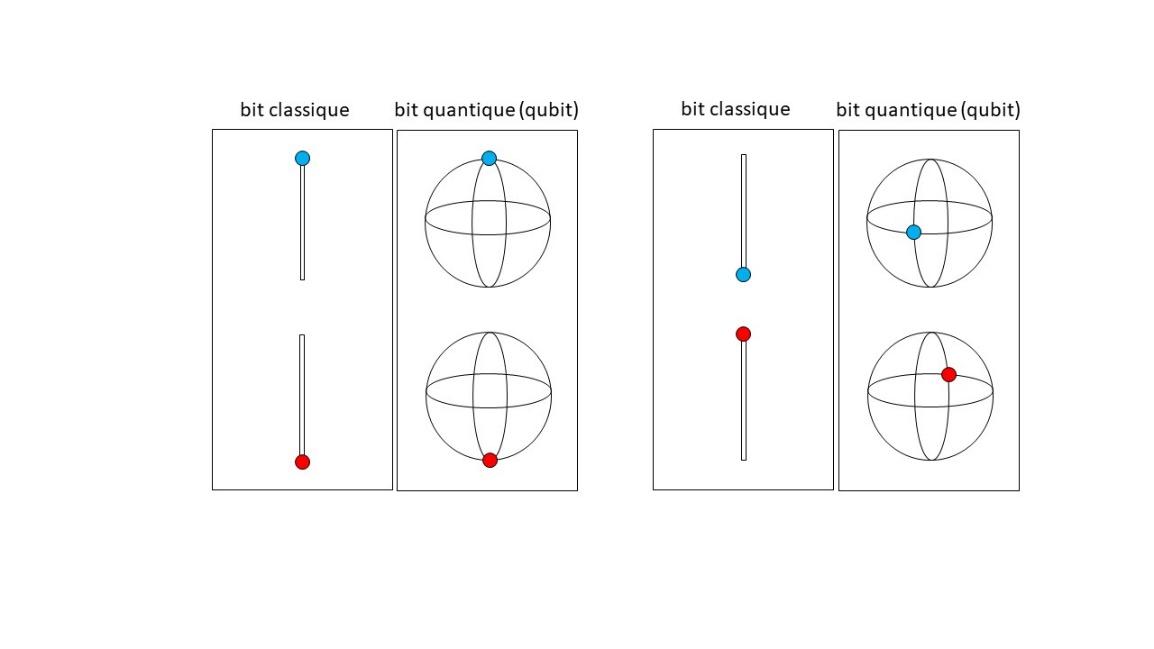
Panneaux de gauche : un bit classique peut se trouver dans deux configurations, représentées par un point forcé de se trouver aux extrémités d’un segment. On colorie en bleu le point si sa configuration représente 0 et en rouge si sa configuration représente 1. Les configurations du qubit, en revanche, sont représentées par deux points antipodaux d’une sphère.
Panneaux de droite : lors d’un changement d’encodage du bit classique, la seule possibilité est d’échanger les rôles de 0 et de 1. Pour le qubit, une variété continue de paires de points antipodaux peut être choisie sur la sphère. Ici, on a représenté une paire de points placés sur l’équateur, mais une latitude et une longitude différentes auraient pu tout aussi bien être choisies. Cette liberté continue des qubits, qui croît exponentiellement avec le nombre de qubits dans un registre, est appelée « principe de superposition ». Elle confère aux qubits une puissance supérieure à celle des bits classiques.
LES DEUX DÉCOUVERTES DE PETER SHOR, PÈRE FONDATEUR DE L’INFORMATION QUANTIQUE MODERNE
Quelques années plus tard, en 1994, coup de théâtre : un mathématicien du MIT à Boston, Peter Shor, propose un nouvel algorithme de la factorisation d’un nombre en ses facteurs premiers. Cette factorisation est très importante, sur le plan à la fois conceptuel et pratique. C’est l’exemple le plus simple d’une fonction asymétrique. Il est très rapide de multiplier deux nombres premiers. En revanche, il est très difficile, en connaissant seulement leur produit, de remonter aux deux nombres de départ. Cette asymétrie est à la base du codage des informations sensibles sur Internet, comme les codes des cartes de crédit, ou les informations médicales. Peter Shor démontre mathématiquement que son nouvel algorithme, qui ne peut être exécuté que par un hypothétique ordinateur quantique, battrait de manière exponentielle le meilleur algorithme classique. À la grande stupeur des informaticiens, ce nouvel algorithme classait la factorisation dans la catégorie des problèmes dits faciles, c’est-à-dire ceux dont le temps d’exécution croît de manière polynomiale en fonction du nombre N de chiffres contenus dans l’énoncé du problème. Les problèmes difficiles sont ceux où le temps d’exécution croît comme une fonction exponentielle de N, ce qui semble être le cas pour la factorisation. La raison de cette stupeur est que l’on croyait jusque-là qu’un algorithme avait une complexité intrinsèque, complexité mesurée par une puissance de N qui était indépendante de la machine sur laquelle l’algorithme était exécuté, même si différentes technologies pouvaient changer un pré-facteur numérique dans l’expression du temps d’exécution.
Mais l’enthousiasme des informaticiens est de courte durée, car il semble alors que la démonstration de Peter Shor de la complexité quantique en N3 de son algorithme quantique implique, pour que l’algorithme fonctionne, que la machine soit parfaite. C’est pour répondre à ce point que Peter Shor conçut une seconde invention, qui allait, elle, véritablement lancer le sujet de l’information quantique : comme les ordinateurs classiques, les ordinateurs quantiques peuvent très bien être construits avec des pièces imparfaites, qui sont donc sujettes à faire des erreurs. Cette deuxième découverte est encore plus extraordinaire que la précédente. Elle est maintenant considérée par certains comme la grande découverte quantique de la fin du XXe siècle. Elle démontre qu’il est possible en théorie de concevoir un processus − dit de correction quantique d’erreurs − qui peut réparer l’influence du bruit et des imperfections du hardware, ce que nombre de physiciens croyaient interdit par les lois de la physique. Ces physiciens se basaient sur le fameux principe d’incertitude d’Heisenberg (encore lui, mais dans un rôle un peu différent), qui semble conférer à la mesure un caractère nécessairement intrusif et aléatoire. Ils objectaient que corriger, c’était prendre connaissance des erreurs, c’est-à-dire effectuer une mesure, qui allait nécessairement entraîner une perturbation, laquelle entraînerait de nouvelles erreurs, de sorte que le processus de correction ne pourrait pas converger.
L’astuce diabolique trouvée par Peter Shor repose, elle aussi, sur un contournement du principe d’incertitude. Il comprend qu’en physique quantique, il est tout à fait possible de détecter qu’une erreur s’est produite dans le système et de savoir où, sans avoir besoin de prendre directement connaissance de l’information qui est encodée, ce qu’un raisonnement classique croit nécessaire (voir en encadré le principe de la correction quantique).
L’AVENTURE DE L’IMPLÉMENTATION DES MACHINES QUANTIQUES
Depuis, différentes équipes de physiciens, dans le monde (USA, Canada, Europe, Chine, Inde, Australie), ont réussi non seulement à réaliser des qubits, mais aussi à les faire interagir pour effectuer des portes logiques. Récemment, l’équipe de mon laboratoire à Yale est parvenue à démontrer que la correction d’erreur pouvait fonctionner en pratique, ce qui est une étape essentielle. Les systèmes les plus performants actuellement sont ceux basés sur les puces de circuits supraconducteurs à base de jonctions Josephson et ceux basés sur des réseaux d’atomes lévités dans le vide. Dans cette dernière approche, les atomes sont contrôlés individuellement par des faisceaux lasers. Il y a d’autres technologies possibles, comme les puces de fibres optiques intégrées et les qubits de spins isolés dans les semi-conducteurs. Personne n’a encore réussi à construire des machines qui dépassent l’ordre de grandeur du millier de qubits interconnectés par des portes quantiques. Ceci est à comparer aux dizaines de milliards de transistors sur une puce d’ordinateur portable… Pourtant, les progrès sont constants, année après année, si on intègre toutes les recherches sur le plan international, financées à hauteur de quelques milliards de dollars par an pour un pays comme les USA (à comparer aux dizaines de milliards par an des investissements dans les puces semi-conductrices). Même si les progrès sont plus lents que ne le voudraient les investisseurs, il n’y a pas eu encore d’« hiver » quantique, comme ce fut le cas en intelligence artificielle, qui a progressé par paliers depuis les années 1960. À ce jour, aucun principe de la physique n’a été découvert qui interdise la réalisation d’un ordinateur quantique de taille arbitraire. Avant de discuter des applications possibles des machines quantiques, approfondissons leurs principes de base et essayons de comprendre l’avantage qu’elles peuvent offrir dans le traitement de l’information.
COMMENT FONCTIONNENT LES QUBITS ET QUELLES SONT LEURS DIFFÉRENCES AVEC LES BITS CLASSIQUES ?
Les journalistes répondent en général à ces questions en commençant par invoquer le principe de superposition. Selon l’expression en vigueur dans les médias, les qubits pourraient être à la fois dans l’état 0 et 1. Cette dernière phrase est une simplification grossière, car la lecture d’un qubit donne toujours un résultat qui ne peut être que 0 ou 1, comme la lecture d’un bit classique.
L’explication correcte des différences entre bit classique et bit quantique fait intervenir la notion de codage, qui est discret dans le cas classique, et continu dans le cas quantique, ce qui permet l’observation d’interférences, car on peut prendre les différents chemins qui existent d’un point à l’autre d’une sphère (voir illustration en page 15).
Plus généralement, il y a plusieurs différences fondamentales entre une machine traitant l’information classique et celle traitant l’information quantique :
- Si l’on répète, avec les mêmes données de départ, le même algorithme − au sens d’une suite de portes logiques − sur une machine classique supposée parfaite, on obtient toujours à la fin le même résultat. Mais si l’on répète le même programme sur une machine quantique, la mesure du résultat final ne donne pas toujours les mêmes valeurs et présente une distribution statistique avec des corrélations d’un type inatteignable par une machine classique.
- La relation entre les données initiales et les données finales obéit à une nouvelle logique, la logique quantique, qui se trouve être celle de la nature, et non pas celle formulée par les mathématiciens grecs de l’Antiquité. La logique classique des Grecs est « dégénérée » par rapport à la logique quantique, qui par exemple, n’interdit pas que les amis de nos amis soient nos ennemis. En effet, les corrélations quantiques n’obéissent pas aux mêmes théorèmes de transitivité que les corrélations classiques.
- L’ordinateur quantique semble tenir sa puissance de l’exploitation du phénomène d’intrication, qui permet à l’information d’être encodée de manière non-locale. Un bit d’information quantique peut, en principe, sans qu’il en soit fait la moindre copie, être délocalisé sur plusieurs machines à la fois, et il pourrait même être simultanément en deux points de la Terre distants de plusieurs milliers de kilomètres (record actuel = plusieurs dizaines de km).
Les propriétés particulières de l’information quantique confèrent à l’ordinateur quantique la capacité de résoudre certains problèmes insolubles par un ordinateur classique, ou de construire des réseaux de communications dont la sécurité est assurée par les lois de la physique. Mais les applications les plus convaincantes de l’information quantique sont celles qui s’appliquent au monde quantique lui-même. La proposition de Feynman a été maintenant confirmée : l’ordinateur quantique pourrait effectuer des calculs pour la conception de nouvelles molécules en chimie et en pharmacologie, et dans la création de nouveaux matériaux. Les machines quantiques de traitement de l’information pourraient aussi s’avérer très utiles aux mesures de grande précision, comme la détection des ondes gravitationnelles, ou bien celles très sensibles portant sur de très faibles quantités de matière, comme l’imagerie des molécules individuelles. Il y a maintenant peu de doute que l’information quantique fournira dans le futur des outils puissants pour la recherche fondamentale.
LES APPLICATIONS INDUSTRIELLES DE L’INFORMATION QUANTIQUE
Les succès remportés dans le monde académique dans la vérification expérimentale des concepts de base de l’information quantique a suscité l’intérêt des grandes compagnies de l’économie numérique (Google, IBM, Intel, Microsoft, Amazon, etc..) et a entraîné la création de plusieurs dizaines de start-up. Est-ce que l’adage : If it is beautiful, it is useful se vérifiera pour la société dans son ensemble ? Si on peut dire qu’une industrie quantique se soit mise d’ores et déjà en place, les espoirs d’applications commerciales à grande échelle restent pour l’instant hypothétiques. Mais le public a déjà constaté que les grandes compagnies de l’Internet bâtissaient elles-mêmes l’environnement social qui les rendait indispensables. Arriveront-elles à faire en sorte, par exemple, que nous ne puissions plus nous passer un jour de jeux et de distractions quantiques ? N’oublions pas non plus que la première application pratique des principes de la physique quantique a été une proposition d’argent quantique basée sur la propriété de l’information quantique de ne pas pouvoir être copiée – en d’autres termes, elle ne peut pas être complètement dématérialisée, même si sa téléportation à grande distance est possible en se servant de l’intrication. Peut-être la véritable application à grande échelle des ordinateurs quantiques est-elle la sécurisation avancée de nos données personnelles ?
La correction d'erreurs quantiques
Prenons d’abord l’exemple d’un bit classique pouvant se retourner aléatoirement de temps à autre, ce qui crée une erreur, appelée bit-flip (on suppose ici que c’est la seule erreur possible). Nous pouvons protéger l’information de la manière suivante. Utilisons trois bits physiques pour coder un bit logique. Le 0 logique sera codé par le triplet physique 000, et le 1 logique sera codé par le triplet physique 111. On voit qu’ainsi, même si une erreur se produit sur un des bits physiques, on pourra récupérer l’information initiale. En effet, si l’on peut être certain qu’un seul bit-flip a lieu, il suffit de compter le nombre de 0 et de 1 dans le triplet pour reconstituer la configuration de départ. Le tableau suivant résume le processus de correction d’erreur. La colonne de gauche indique ce que l’on a lu dans le registre, et la colonne de droite la valeur après correction.
|
000 |
→ |
000 |
|
001 |
→ |
000 |
|
010 |
→ |
000 |
|
100 |
→ |
000 |
|
110 |
→ |
111 |
|
011 |
→ |
111 |
|
101 |
→ |
111 |
|
111 |
→ |
111 |
Mais en mécanique quantique, on ne peut pas utiliser cette stratégie. Même si le passage de 1 à 3 qubits est bénéfique (redondance), lire directement le contenu informationnel du qubit détruit l’information quantique, suivant le principe d’incertitude. Il faut ruser. La solution est de mesurer la somme modulo 2 (appelée ici S12) des deux premiers qubits, puis la somme modulo 2 (appelée ici S23) des deux derniers qubits. Ainsi, on obtient l’information nécessaire pour corriger le qubit fautif, sans avoir à lire directement l’information. Le tableau ci-dessous examine les quatre cas possibles de résultats pour la mesure des deux sommes modulo 2, qui ne perturbe pas les qubits.
|
S12 = 0, S23 = 0 |
→ |
ne rien faire |
|
S12 = 0, S23 = 1 |
→ |
flipper qubit 3 |
|
S12 = 1, S23 = 0 |
→ |
flipper qubit 1 |
|
S12 = 1, S23 = 1 |
→ |
flipper qubit 2 |
On a supposé ici qu’il ne se produisait qu’un seul bit-flip quantique dans le triplet. Ici, le flip de qubit correspond à une rotation de la sphère de la figure ci-avant autour d’un axe passant par l’équateur. Mais on peut aussi avoir une erreur dite de phase-flip, correspondant à une rotation autour d’un axe passant par le pôle. Si on veut corriger à la fois les deux types d’erreur, bit-flips et phase-flips, il faut encore plus de redondance. Le code historique inventé par Peter Shor comprenait neuf qubits. Des recherches plus récentes ont montré que le minimum théorique est cinq qubits physiques pour un qubit logique. Des codes de correction d’erreur plus sophistiqués, ont été inventés théoriquement, comme le code dit de « surface » comprenant des centaines de qubits par qubit logique. Dans ces derniers codes, sont protégées des erreurs non seulement la mémoire, mais aussi les opérations logiques. Au moment où cet article est rédigé, protection des opérations logiques, clé de voûte des applications de l’ordinateur quantique, reste à mettre en œuvre sur le plan pratique.
En savoir plus
Julien Bobroff, "La nouvelle révolution quantique", Flammarion, 2022
Carlo Rovelli, "Helgoland", Champs, 2023
Scott Aaronson, "Quantum computing since Democritus", Cambridge University Press, 2013
Assa Auerbach, "Max the demon", Amazon, 2017

Michel DEVORET (1975)
Après avoir suivi, en dernière année à Télécom, le DEA d’Optique Quantique, Physique Atomique et Moléculaire de l’Université Paris XIII Orsay, Michel Devoret a soutenu sa thèse de 3e cycle dans ce domaine, puis il a bifurqué vers la physique du solide pour sa thèse de Doctorat d’État dans la même université. Après un séjour de post-doctorat à l’Université de Californie de Berkeley, il a fondé son propre groupe de recherche sur les circuits quantiques supraconducteurs au CEA-Saclay, avec Daniel Esteve et Cristian Urbina. En 2002, il devient professeur à l’Université de Yale. Il a aussi enseigné au Collège de France de 2007 à 2012. Michel Devoret est membre de l’Académie des Sciences (France) et de la « National Academy of Sciences » (USA).
Auteur